非常高效的解决连接问题
判断网络中节点的链接状态
数学中集合并的实现
并查集的定义
- 判断是否连接,只需要判根节点是否一样
指向树的根节点
并查集主要实现的方法:
- 判断是否连接isConnected
- 把两个集合并起来
Quick Find
设计思想:定义一个数组,给里面每个值定义一个标识符,标识是否在一个集合中;并操作,如果不在一个集合中,使用for循环让他们的标识符一致,这就形成了并操作
具体实现: 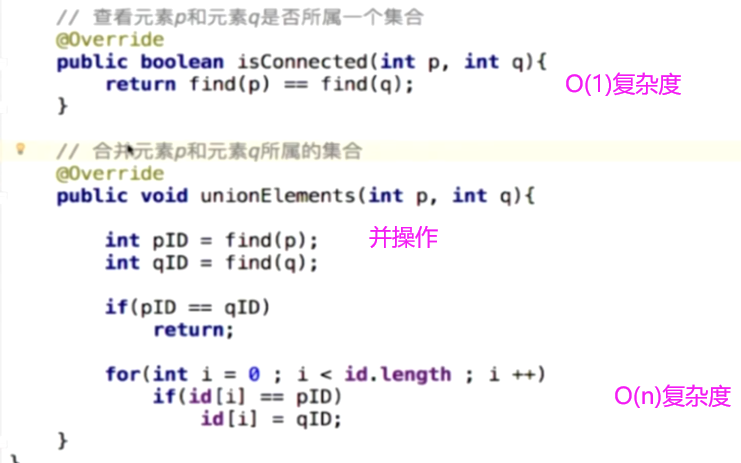
Quick Union
改善并操作O(n)的时间复杂度,使用树来实现平均复杂度为O(logn)
设计思想:将每一个元素看作一个节点,判断是不是连接,就判断他们的指向的根节点是否一样;并操作:将这个树的根节点指向另一棵树的根节点即可;
具体实现:初始化数组,使每个元素指向它自己
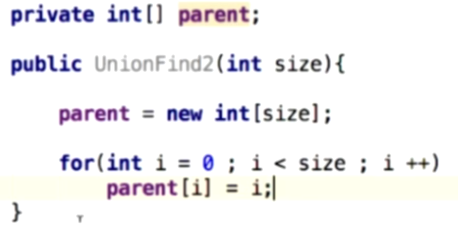
find方法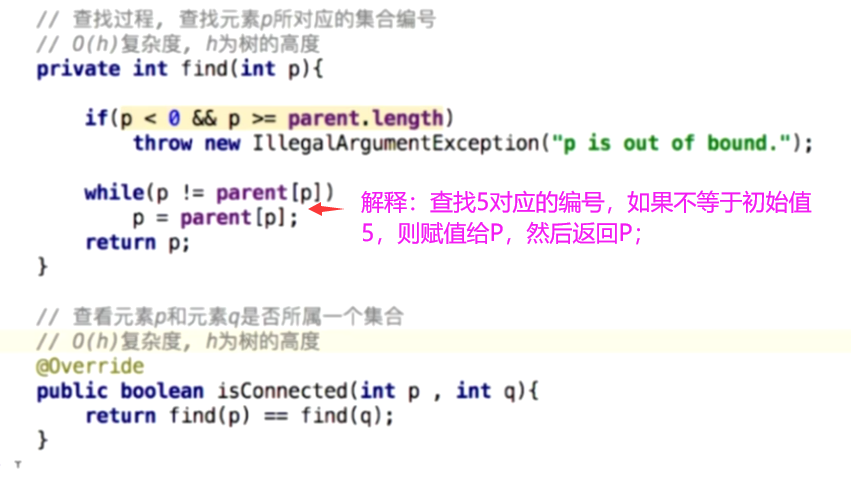
find方法因为是树形结构所以查找过程中不是相邻的,是索引的查找,需要在不同的地址之间跳转;
union操作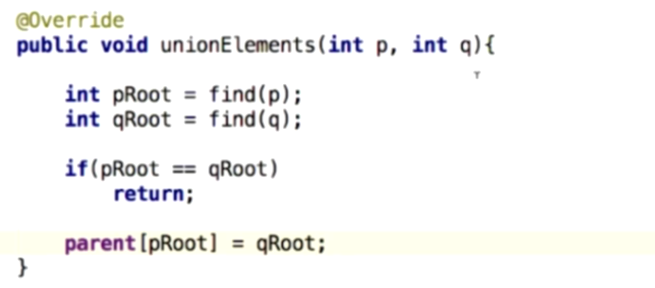
缺点:这棵树可能会很大,很深;时间复杂度很高
优化:考虑size;将高度低的那棵树指向高度高的那棵树,这样来控制树的高度;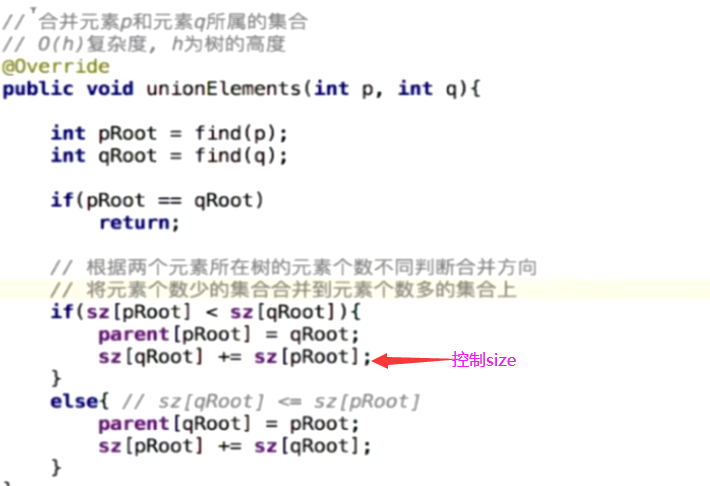
性能提升大概500倍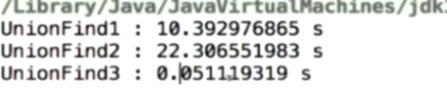
让9指向8而不指向4的原因是:防止成为链表
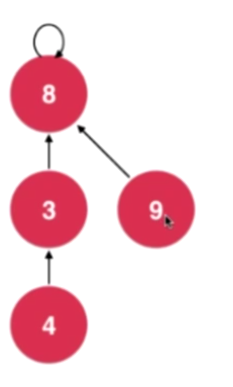
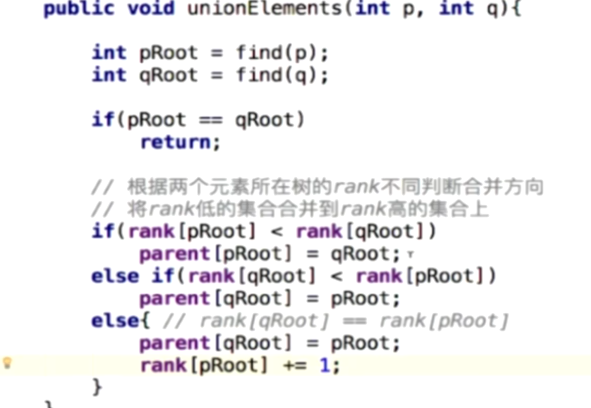
基于RANK的优化
rank[i]表示根节点为I的树的高度;
路径压缩
1 | parent[p] = parent[parent[p]]; |
设计思想:让该节点指向父亲节点的父亲节点,以降低树的高度;
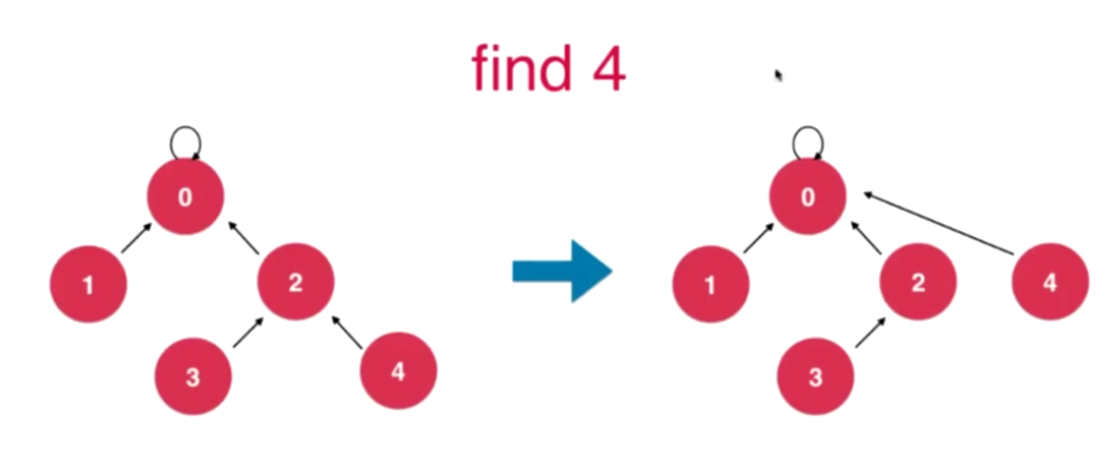
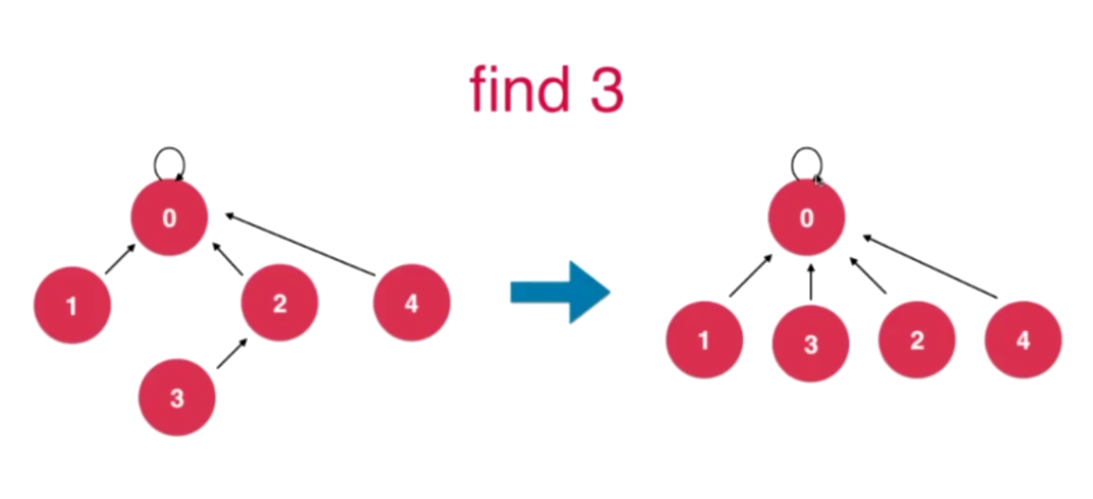
递归实现:
时间复杂度分析
并不是严格意思上的二叉树,所以时间复杂度做了解即可

总结:树结构的变种堆、线段树、trie、并查集;
Others:
- leetcode