AVL中平衡二叉树定义:对于任意一个节点,左子树和右子树的高度差不能超过1
eg:满二叉树,完全二叉树,线段树
标注节点的高度
计算平衡因子:左右子树高度差相减;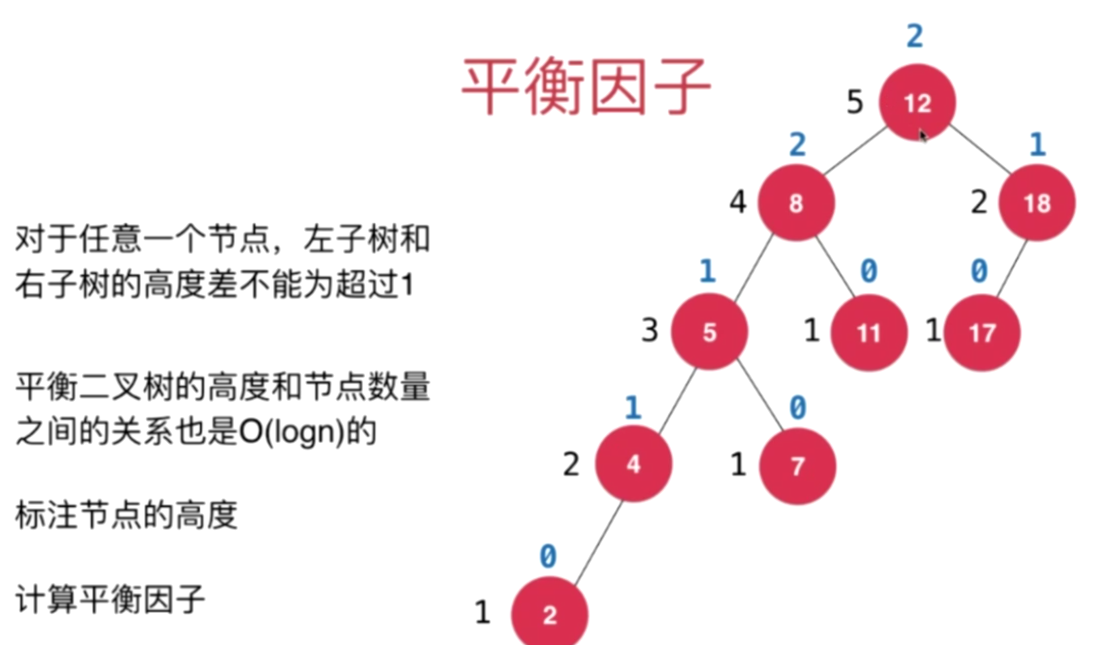
判断是否为平衡二叉树并计算平衡因子
在数据插入时维护二叉树平衡
右旋转原理:插入的元素在不平衡的节点的左侧的左侧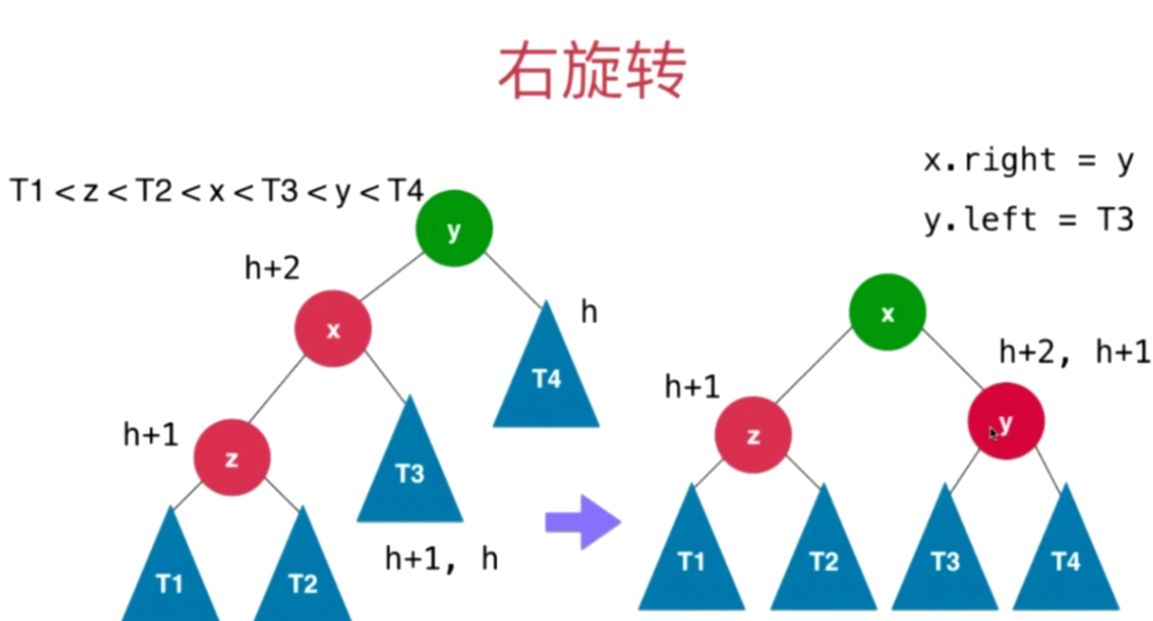
旋转之后既维持了二分搜索树的性质又实现了平衡;
方法实现: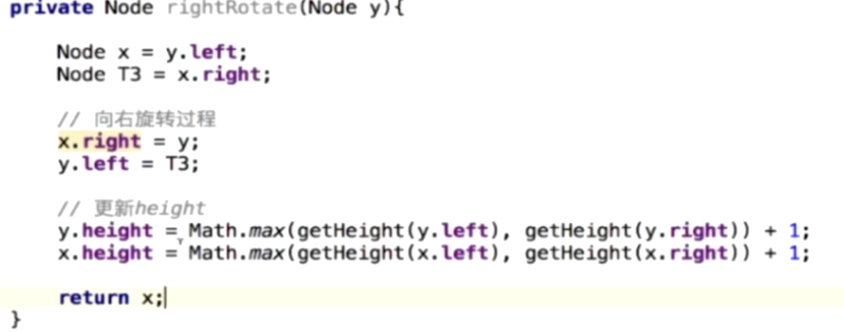
左旋转:插入的元素在不平衡的节点的右侧的右侧
1 | x.left = y; |
当节点都比X大时,不能单纯的进行左旋转右旋转
LL(左旋转):
RR(右旋转):
LR(先左旋转后右旋转):
插入的元素在不平衡的节点的左侧的右侧
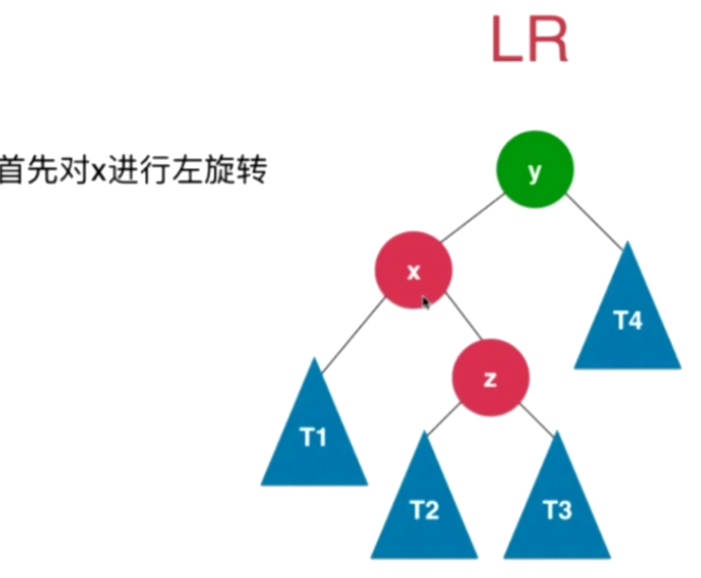
- 转化成了LL的情况
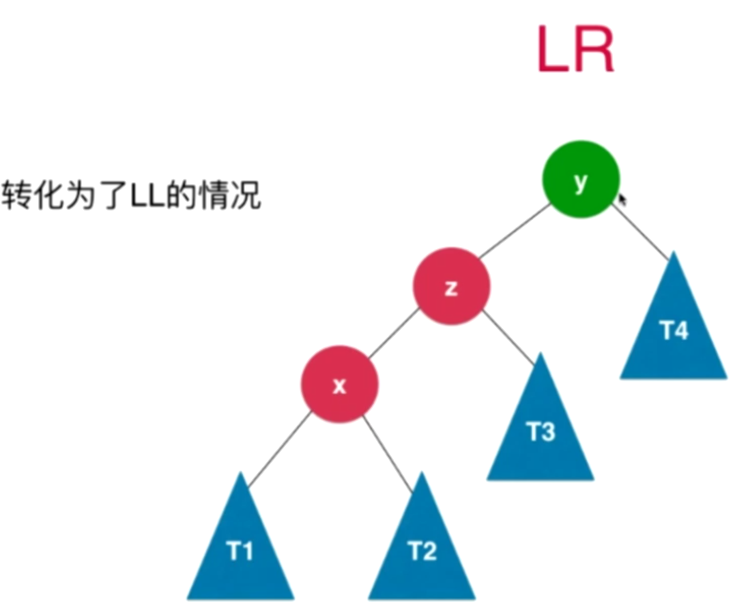
- 转化成了LL的情况
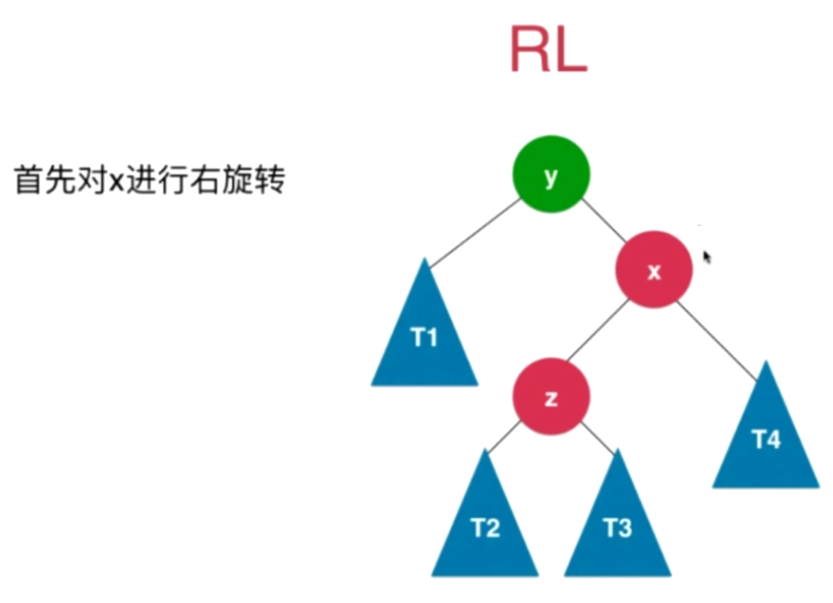
RL(先右旋转后左旋转):
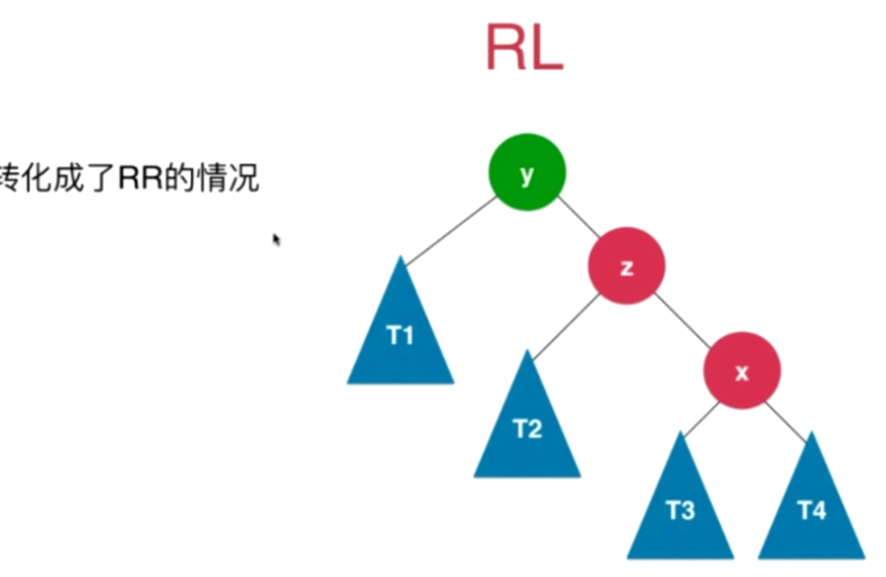
- 添加的节点在不平衡节点的右子树的左侧,先对右节点进行右旋转化为RR,然后对RR进行左旋转
- 转换成RR的情况
删除元素
删除一个元素后,会往上回溯
和BST删除一样,remove之后会返回一个根节点,再对这个node进行平衡得到平衡的node;
会有点耗时,因为每次删除完都要平衡遍历;
基于AVL树的Set和Map
AVL树的局限性
红黑树和AVL树的时间复杂度一致,但是红黑树旋转操作更少;