为什么要有线段树?比如现在有一个数组,要计算和查赵这个数组中某个区间的值的和,那么它的时间复杂度就是O(n),要遍历数组;而如果使用树结构,他的时间复杂度为O(logn);差距还是很大的
什么是线段树?
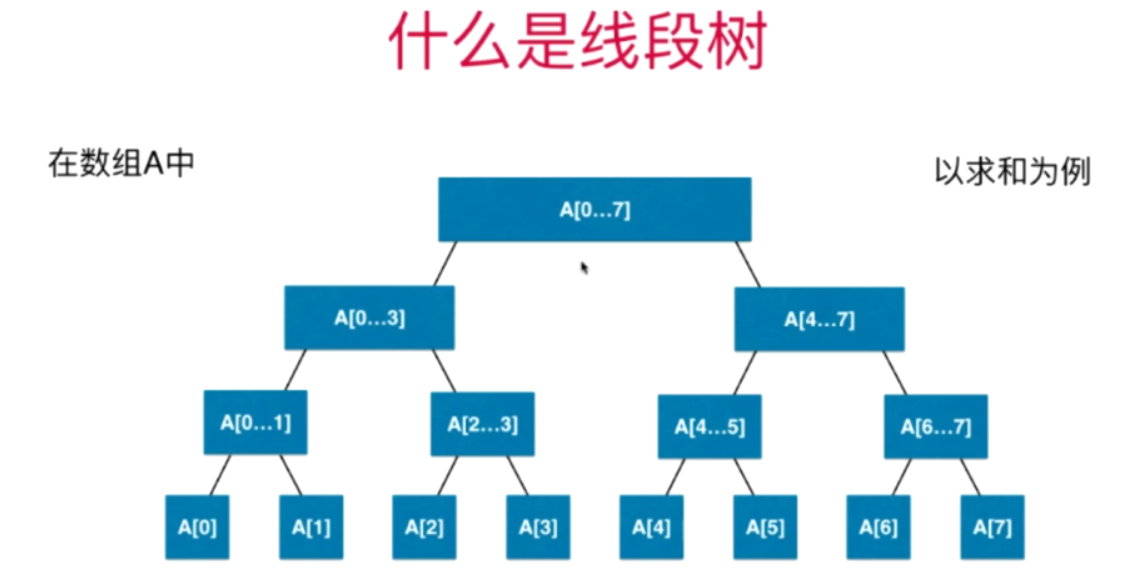
特点:
线段树不是完全二叉树
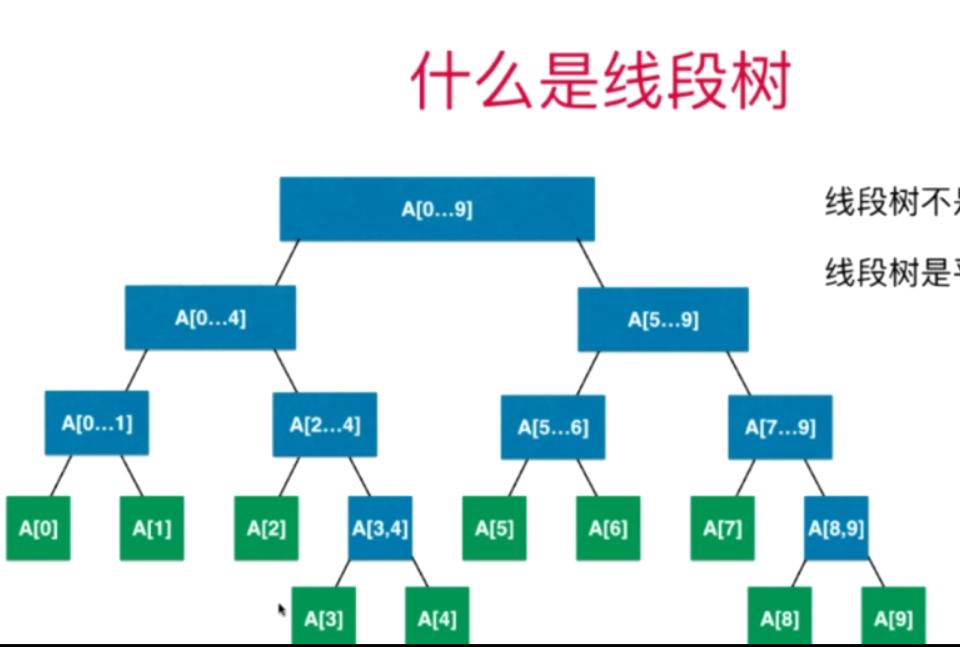
线段树也是平衡二叉树
用数组实现,开辟空间,定义左子树和右子树
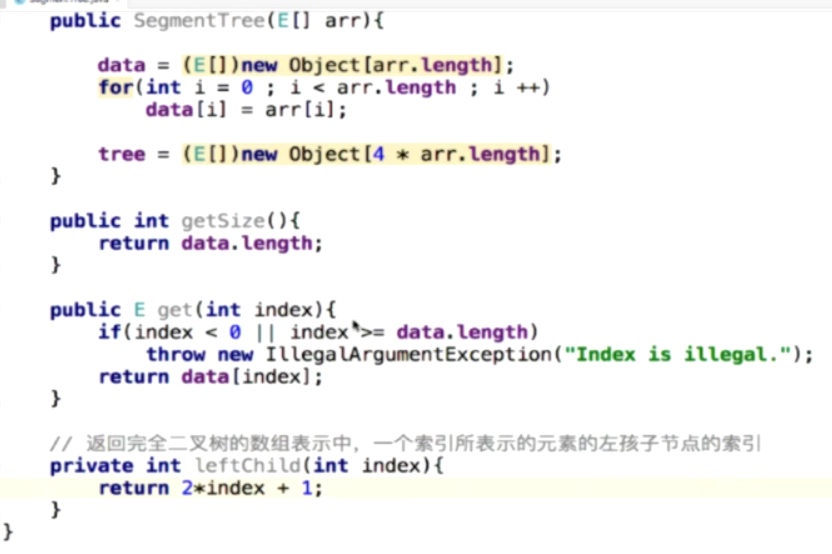
创建线段树: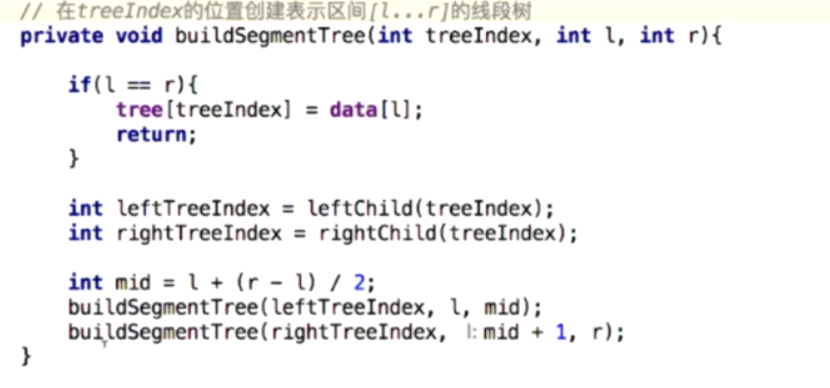
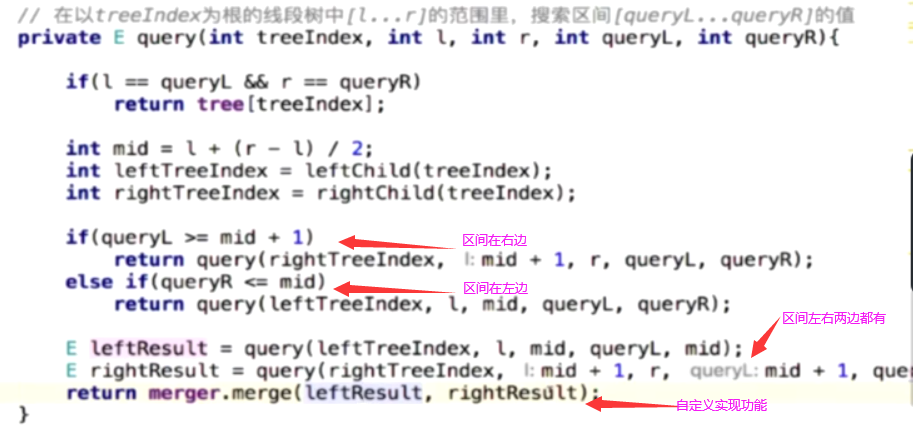
线段树的区间查询操作
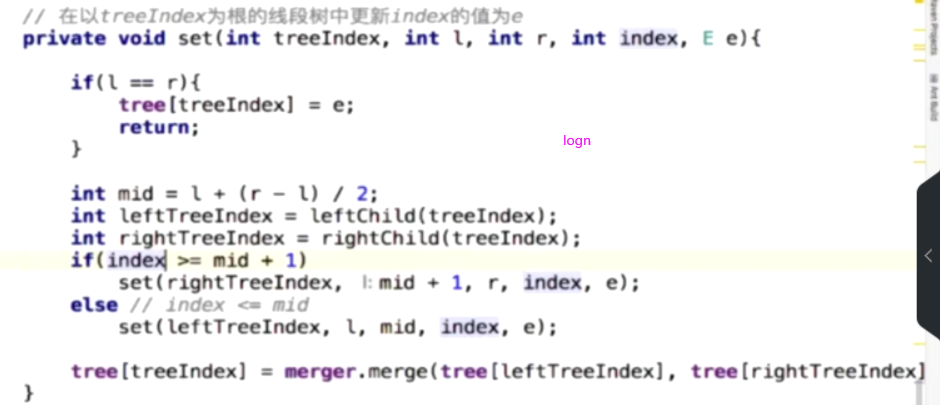
线段树的更新操作
Lazy更新
链式动态线段树
不浪费空间
时间复杂度

Others:
- leetcode第303题区域和检查
- leetcode第307题区域和检查美版UPDATe
- 树状数组(了解)BIT
- RMQ问题