经典红黑树

红黑树

先介绍下2——3树

2-3树

性质：

• 满足二分搜索树的基本性质
• 节点可以存放一个或者两个元素
• 
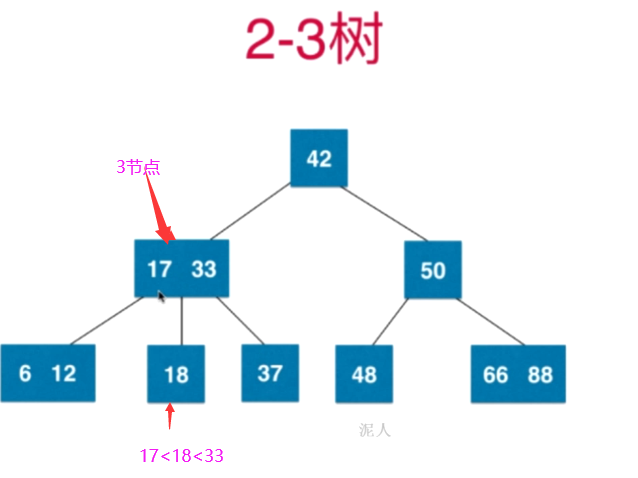
• 2-3树是一棵绝对平衡的树

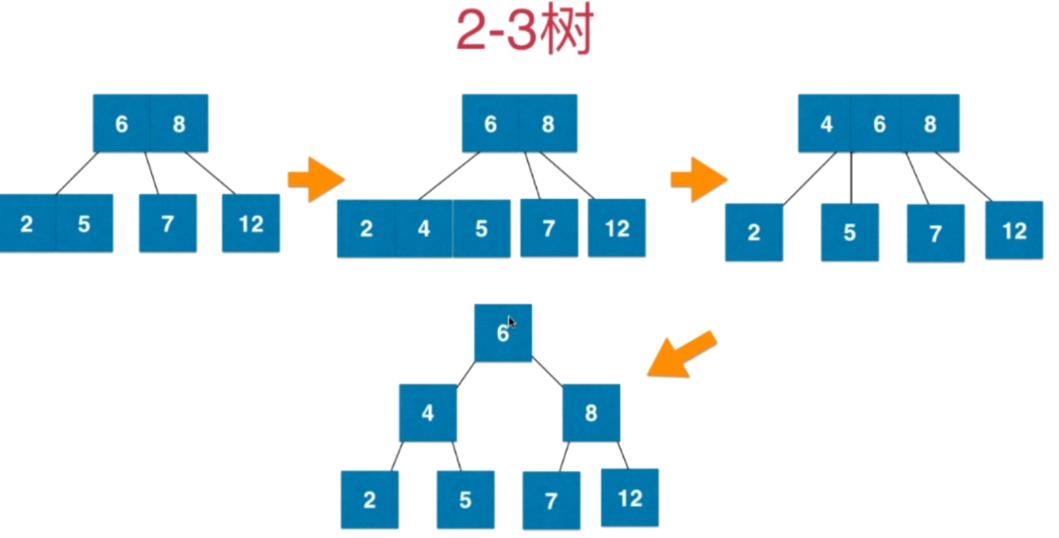
2-3树如何维持绝对平衡的？

​ 在插入数据的时候不会放在null的位置，if null就和parent节点暂时相融合变成3节点或者4节点如图：

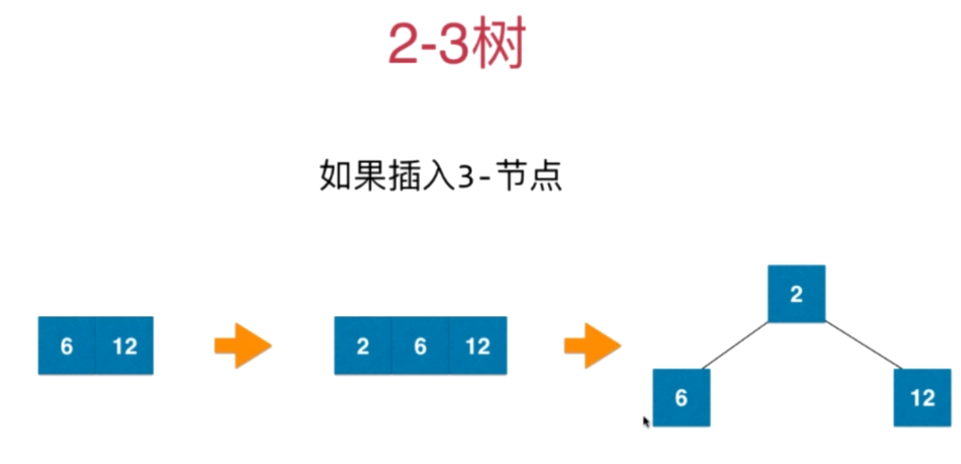
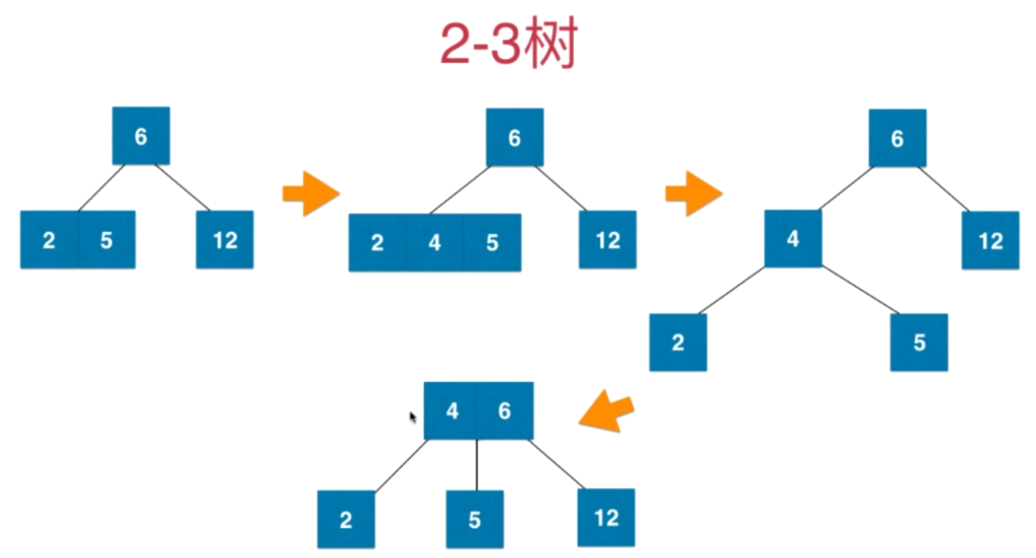
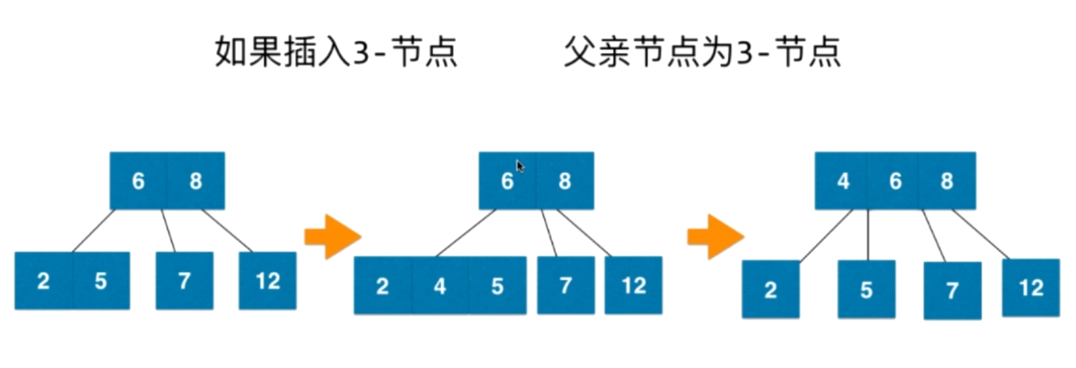
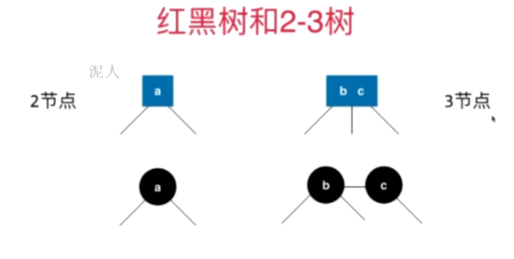
红黑树与2-3树的等价性

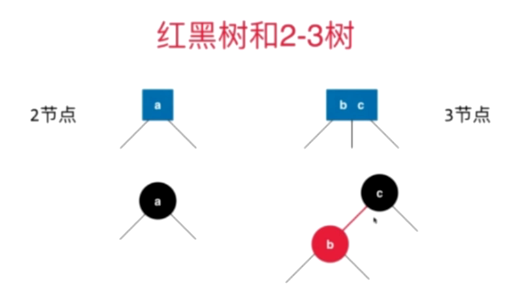
b—c连接线变成红色的b变为红色的

定义一个红黑树

public class RBTree<K extends Comprarable<K>, V>{
    private static final boolean RED = true; 
    private static final boolean BLACk = false;
    private class Node{
        public K key;
        public V value;
        public Node left,right;
        public boolean color;
        public Node(K key,V value){
            this.key = key;
            this.value = value;
            left = null;
            right = null;
            color = RED;//默认创建的节点为红色
        }
    }
}

《算法导论》中的红黑树

1. 每个节点或者是红色的，或者是黑色的；
2. 根节点是黑色的；
3. 每个叶子节点（最后的空节点）是黑色的；
4. 如果一个节点是红色的，那么它的孩子节点是黑色的；
5. 从任意一个节点到叶子节点，经过的黑色节点是一样的；

保持“黑平衡”的二叉树，严格意义上，不是平衡二叉树；

最大高度：2logn时间复杂度还是O(Logn)

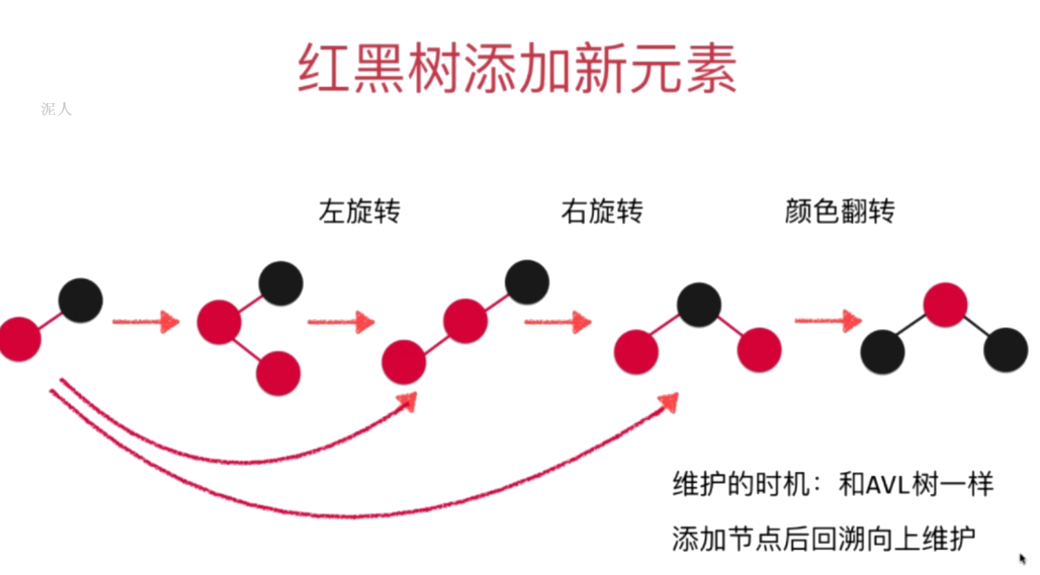
红黑树中添加元素

• 红黑树添加新元素（了解）

红黑树的性能总结

• 对于完全随机的数据，普通的二分搜索树很好用；
• 对于查询较多的使用情况，AVL树很好用；
• 红黑树牺牲了平衡性（2logn的高度）

统计性能更优（增删改查平均情况下更优）

​ 整个红黑树的查找，插入和删除都是 O (logN) 的，原因就是整个红黑树的高度是 logN，查找从根到叶，走过的路径是树的高度，删除和插入操作是从叶到根的，所以经过的路径都是 logN。

红黑树的底层应用

• linux 中进程的调度用的是红黑树；
• Java 中 HashMap、TreeMap、TreeSet（都在内存中操作）也都是用红黑树实现；

Other

• 好文：数据结构之红黑树